 The k-D Tree Structure
The k-D Tree Structure Calculating Gravity
Calculating Gravity Periodic Boundary Conditions
Periodic Boundary Conditions Parallel Aspects of the Code
Parallel Aspects of the Code Domain Decomposition
Domain Decomposition Parallel tree-walking phase
Parallel tree-walking phase The Machine Dependent Layer
The Machine Dependent Layer The k-D Tree Structure
The k-D Tree Structure Calculating Gravity
Calculating Gravity Periodic Boundary Conditions
Periodic Boundary Conditions Parallel Aspects of the Code
Parallel Aspects of the Code Domain Decomposition
Domain Decomposition Parallel tree-walking phase
Parallel tree-walking phase The Machine Dependent Layer
The Machine Dependent LayerThe central data structure in PKDGRAV is a tree structure which forms the hierarchical representation of the mass distribution. Unlike the more traditional oct-tree used in the Barnes-Hut algorithm, we use a k-D tree2, which is a binary tree. The root-cell of this tree represents the entire simulation volume. Other cells represent rectangular sub-volumes that contain the mass, center-of-mass, and moments up to hexadecapole order of their enclosed regions.
To build the k-D tree, we start from the root-cell and bisect recursively the cells through their longest axis. At the very top of the tree we are domain decomposing among the processors, so the bisection is done such that each processor gets an equal computational load. The computational cost is calculated from the previous timestep. Once we are within a processor, each cell is bisected so that the sub-volumes are of equal size so that higher order moments of cells are kept to a minimum (Figure 1). The depth of the tree is chosen so that we end up with at most 8 particles in the leaf cells (buckets). We have found this number to be near optimal for the parallel gravity calculation.

PKDGRAV calculates the gravitational accelerations using the well
known tree-walking procedure of the Barnes-Hut algorithm3, except that it collects interactions for entire buckets
rather than single particles. Thus, it amortizes the cost of tree
traversal for a bucket, over all its particles.
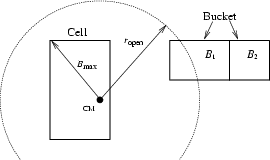
In the tree building phase, PKDGRAV assigns to each cell of the tree
an opening radius about its center-of-mass. This is defined as,
The opening radii are used in the Walk phase of the algorithm as
follows: for each bucket
![]() ,
PKDGRAV starts descending the
k-D tree, ``opening'' those cells whose
,
PKDGRAV starts descending the
k-D tree, ``opening'' those cells whose
![]() intersect with
intersect with
![]() (Figure 2). If a cell is ``opened,''
then PKDGRAV repeats the intersection-test with
(Figure 2). If a cell is ``opened,''
then PKDGRAV repeats the intersection-test with
![]() for the
cell's children. Otherwise, the cell is added to the particle-cell interaction list of
for the
cell's children. Otherwise, the cell is added to the particle-cell interaction list of
![]() .
When PKDGRAV reaches
the leaves of the tree and a bucket
.
When PKDGRAV reaches
the leaves of the tree and a bucket
![]() is opened, all
of
is opened, all
of
![]() 's particles are added to the particle-particle
interaction list of
's particles are added to the particle-particle
interaction list of
![]() .
.
 |

Experience has shown that using a data structure for the domain
decomposition that does not coincide with the hierarchical tree for
gravity calculation, leads to poor memory scaling with number of
processors and/or tedious book-keeping. That is the case, for
instance, when using an Orthogonal Recursive Bisection (ORB) tree for
domain decomposition and an oct-tree for gravity7.
Current domain decomposition techniques for the oct-tree case involve
forming ``costzones,'' that is, processor domains out of localized
sets of oct-tree cells8, or ``hashed oct-trees''9. PKDGRAV uses the ORB tree structure to represent the
domain decomposition of the simulation volume. The ORB structure is
completely compatible with the k-D tree structure used for the gravity
calculation (Figure 1). A
root finder is used to recursively subdivide the simulation volume so
that the sums of the work-factors in each processor domain are equal.
Once this has been done, each processor builds a local tree from the
particles within its domain. This entire domain decomposition and
tree building process is fully parallelizable and incur negligible
cost to the overall gravity calculation.
The Walk phase starts from the root-cell of the domain
decomposition tree (ORB tree), each processor having a local copy of
this tree, and descends from its leaf-cells into the local trees
stored on each processor. PKDGRAV can index the parent, sibling and
children of a cell. Therefore, it can traverse a k-D tree stored on
another processor in an architecture independent way. Non-local cells
are identified uniquely by their cell index and their domain number
(or processor identifier). Hence, tree walking the distributed data
structure is identical to tree walking on a single processor, except
that PKDGRAV needs to keep track of the domain number of the local
tree upon which the walk is performed. Interaction lists are
evaluated as described earlier, making Walk the only phase where
interprocessor communication takes place, after the domain
decomposition.
On distributed memory machines, such as workstation clusters and IBM's
SP-2, we maintain a local software cache on each processor. When a
processor requests a cell or particle that is not in its cache, the
request is sent to the appropriate processor that owns the data.
While waiting for the data to be sent back, the requesting processor
handles cache-requests sent from other processors. The owner
processor sends back a cache line comprised of more than a single cell
or particle, in an attempt to amortize the effects of latency and
message passing overhead. This cache line is inserted into the local
cache, and a pointer to the requested element is returned. To improve
responsiveness of the software cache, after a number of accesses to the
cache MDL checks whether any requests for data have arrived; if so, it
services these first.
